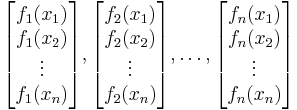Unisolvent functions

In mathematics, a collection of n functions ƒ₁, ƒ₂, ..., ƒ_n is unisolvent on domain Ω if the vectors

$\begin{bmatrix}f_1(x_1) \\ f_1(x_2) \\ \vdots \\ f_1(x_n)\end{bmatrix}, \begin{bmatrix}f_2(x_1) \\ f_2(x_2) \\ \vdots \\ f_2(x_n)\end{bmatrix}, \dots, \begin{bmatrix}f_n(x_1) \\ f_n(x_2) \\ \vdots \\ f_n(x_n)\end{bmatrix}$

are linearly independent for any choice of n distinct points x₁, x₂ ... x_n in Ω. Equivalently, the collection is unisolvent if the matrix F with entries ƒ_i(x_j) has nonzero determinant: det(F) ≠ 0 for any choice of distinct x_j's in Ω.

Unisolvent systems of functions are widely used in interpolation since they guarantee a unique solution to the interpolation problem. Polynomials are unisolvent by the unisolvence theorem

Examples:

1, x, x² is unisolvent on any interval by the unisolvence theorem
1, x² is unisolvent on [0, 1], but not unisolvent on [−1, 1]
1, cos(x), cos(2x), ..., cos(nx), sin(x), sin(2x), ..., sin(nx) is unisolvent on [−π, π]

Systems of unisolvent functions are much more common in 1 dimension than in higher dimensions. In dimension d = 2 and higher (Ω ⊂ R^d), the functions ƒ₁, ƒ₂, ..., ƒ_n cannot be unisolvent on Ω if there exists a single open set on which they are all continuous. To see this, consider moving points x₁ and x₂ along continuous paths in the open set until they have switched positions, such that x₁ and x₂ never intersect each other or any of the other x_i. The determinant of the resulting system (with x₁ and x₂ swapped) is the negative of the determinant of the initial system. Since the functions ƒ_i are continuous, the intermediate value theorem implies that some intermediate configuration has determinant zero, hence the functions cannot be unisolvent.

References

Philip J. Davis: Interpolation and Approximation pp. 31–32